HOW TO CROSS STREETS

Dangerously vibecoded pedestrian street crossing simulation progress notes

EDIT 2: FAQs (F being n=1, thanks Alex) at the bottom

If you're in a manhattan-grid type city situation and need to walk to a diagonal destination, and street crossings have pedestrian signals, what's the optimal way to navigate?

Don't know since math can only be right about MODELS of the world, and simulation is for cowards too afraid to do REAL math, BUT...

Here's the grid:

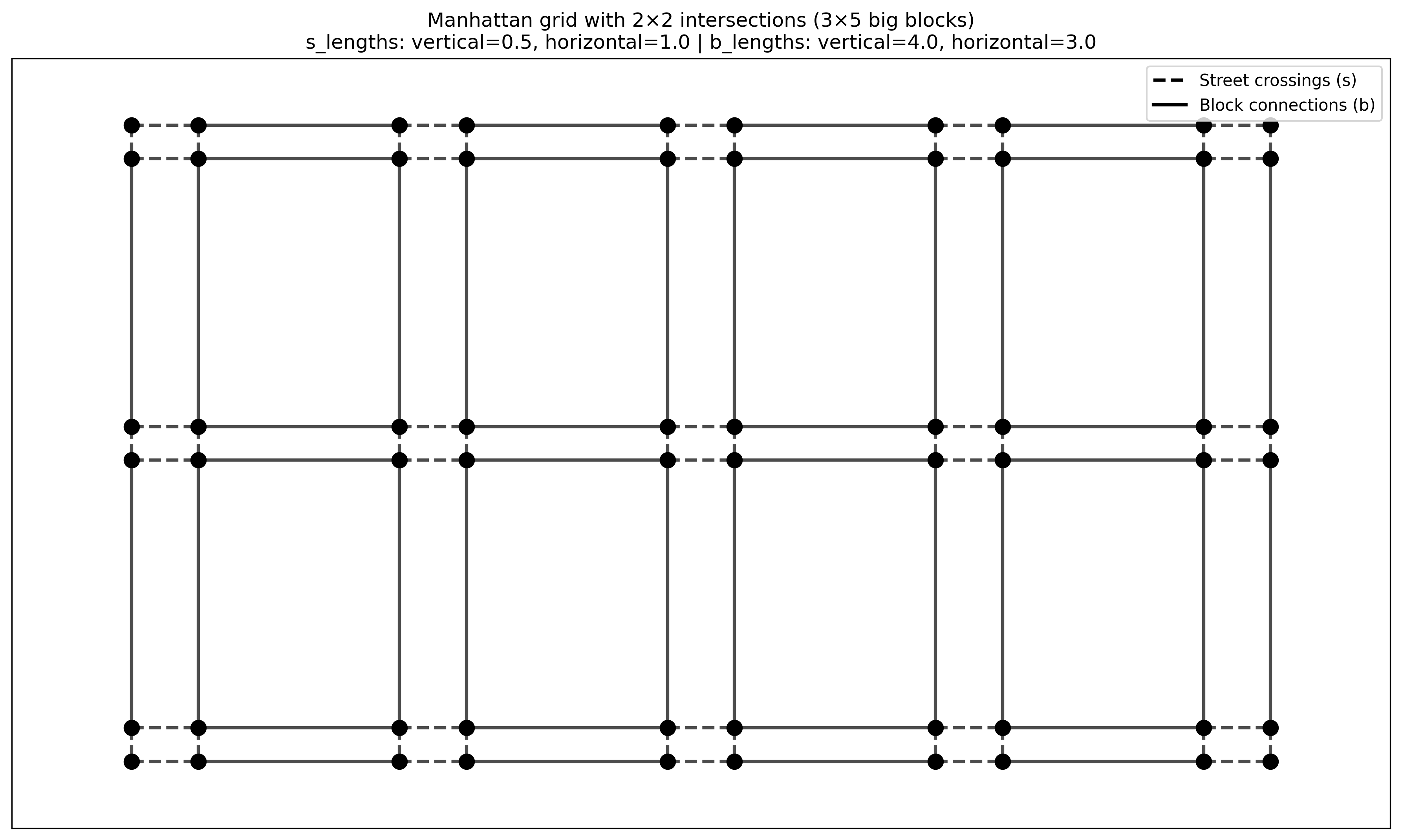
We're going from the top left to the bottom right, potentially stopping at each of the dashed lines: we have to wait for the lights at street crossings and can just GO in block crossings.

Pedestrian signals i.r.l. are NOT random — (also that em-dash is NOT AI, I typed two hyphens and substack merged them for me, thanks :^) cities sync traffic signals to make cars flow better, and pedestrian signals are linked. In this v1 simulation, I just model the signals as essentially whether a signal-specific offset i.i.d ~ uniform(0,2), plus the current time, mod 2 is less than 1, later I might simulate syncing.

(imagine a 1 second off, 1 second on pulse with a random starting time for each signal)

What's the ideal strategy? You really only have to make a choice in three situations: take the top left little 2x2 grid of points: at the very top left (where we start), we can either go down or right (potentially waiting for the signal). At the top right (of that 2x2 grid), we could zip rightwards to the next 2x2 grid, or potentially go downwards (if the pedestrian light allows us, or maybe we'd wait until we can go downwards, standing around, wasting time?).

At the bottom right of the 2x2 grid, we could go downwards or rightwards, both directions just zipping along, unbuffeted by the man.

My thinking: at least better than random, we should prioritize being in a spot where we'd keep the most optionality — avoid getting into the edge where we won't be able to choose going right or down. That means this spot:

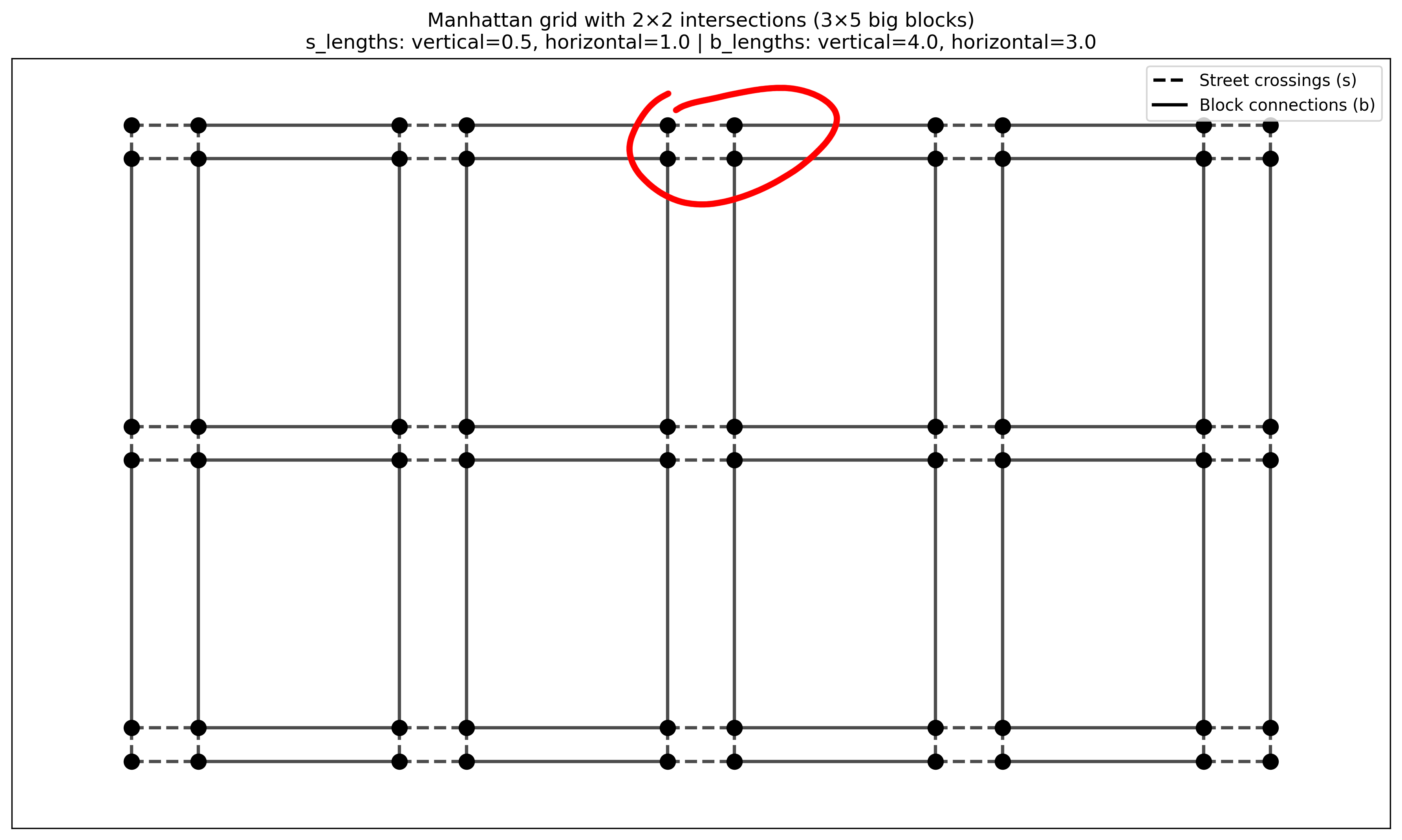
Is highly desirable, and I deliberately chose a non square grid.

So let's consider a walker, and their possible direction-picking strategies:

(Turd in a haversack, substack's codeblocks are TRASH, see [1] for the strategy code at the bottom)

1. random: does what it says on the tin
2. edge: GO EAST, until you can't
3. ORACULAR random: in a perfect paradise, we can actually see the wait times on pedestrian signals (although i.r.l. you can kinda infer it), so pick the lower wait time direction to go in (if they're both green go random)
4. option maximizer: the cleverest, the most beautiful: balance the remaining moves after the next step. If there would be more rightwards moves, go down, and vice versa.

Here are the empirics (2002 possible paths in a 3x5 grid, ran 50000 simulations)

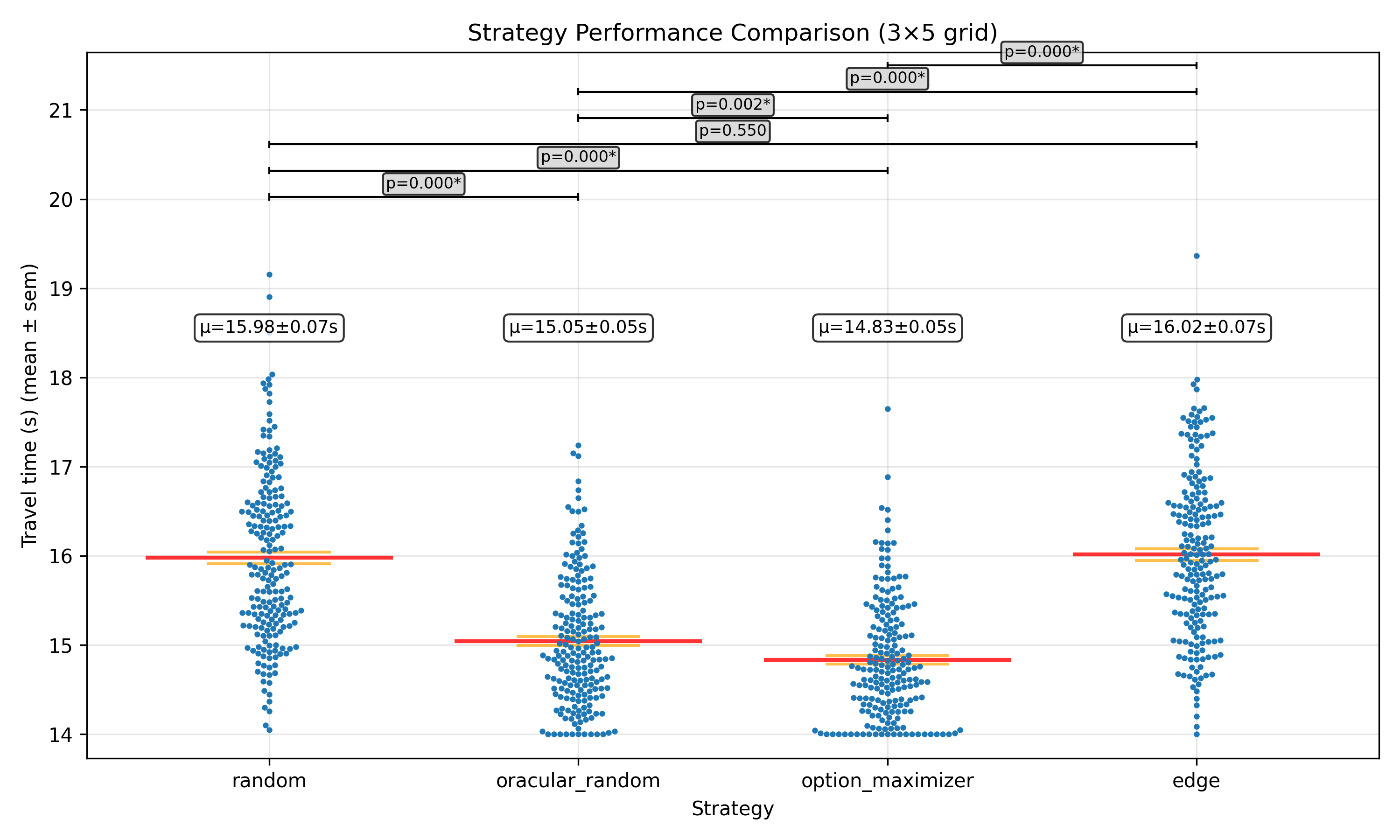
So option_maximizer wins, although I think that a oracular strategy that ALSO does an option maximization would be even better.

Why??

Look at the actual paths taken by random:

This looks asymmetrical and weird — but note, the node visit frequencies at (looking at the top left 2x2) are symmetrical (25102 ~ 24898). It's the overall path usage frequency that's weird. We get to the bottom left corner 1526 times, and the corresponding middle right corner 1550 times (look for that node!), but once we're at the bottom left, we HAVE to go right over and over again, so less path diversity (so the line is thicker) AND we're at the mercy of that rightwards signal chain — we don't have the option to go down if the rightwards light is red. This is sorta like a Galton Board, where you magically end up in paths with more random entry points, but backwards. (this point makes sense in my head, and that's enough).

And as for the option maximizer:

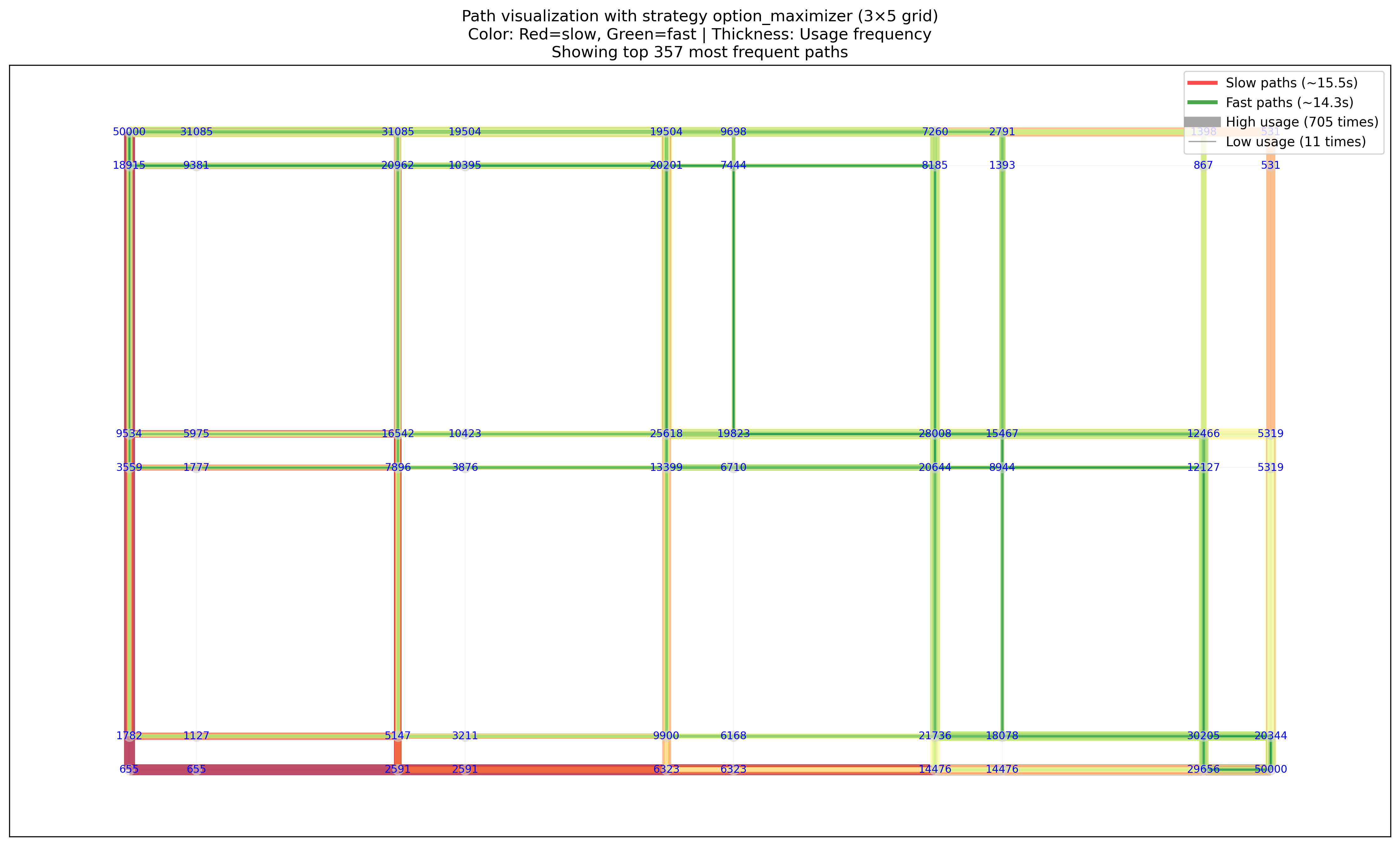
Look at the top left-ish node with 31085 visits: once we're there, we NEVER go downwards. Even if the light might be green, we go rightwards, since we're SPRINTING to the point in the middle (that red circle from before) where we would have lots of rightwards or downwards options, so we never get stuck in the mercy of single option walks.

Other strategies at [2].

There are other strategies to compare, like oracular but also option maximizing, or like option maximizing but a bit chiller about it, far-lookers (that see the next intersection), and more simulation params to look at (very very large grids? synchronized lights? different speeds and distances? right now we're walking at 1 m/s, and the units of the very first graph were in meters).

Also re the vibe coding: I checked the outputs. Also also: lots of the AI responses were kinda trash, like they kept forgetting that there was a BIG grid and a LITTLE grid at each node. Yes I used the fancy expensive water-depriving versions of your-favorite-company's-favorite-product. At least they know matplotlib and seaborn better than any human, mostly because python's plotting is TRASH, STILL.

In conclusion, this was the manic response to an imaginary shower argument I had in my head — no one human being has EVER disagreed with me that my option maximizing strategy is good, although I'm not sure I ever brought it up.

I'll update and expand and fix this stuff (maybe find errata too — this could all be wrong) if people ask for it. As for now, here's the source [3].

EDIT 3: check this out WAOOW.

EDIT 1: obviously lots of more experiments I can do, but right now this website is just a reflexive regurgitant of my brain and I'll update this if I feel like it.

[2] Other strategies

LIVIN ON THE EDGE

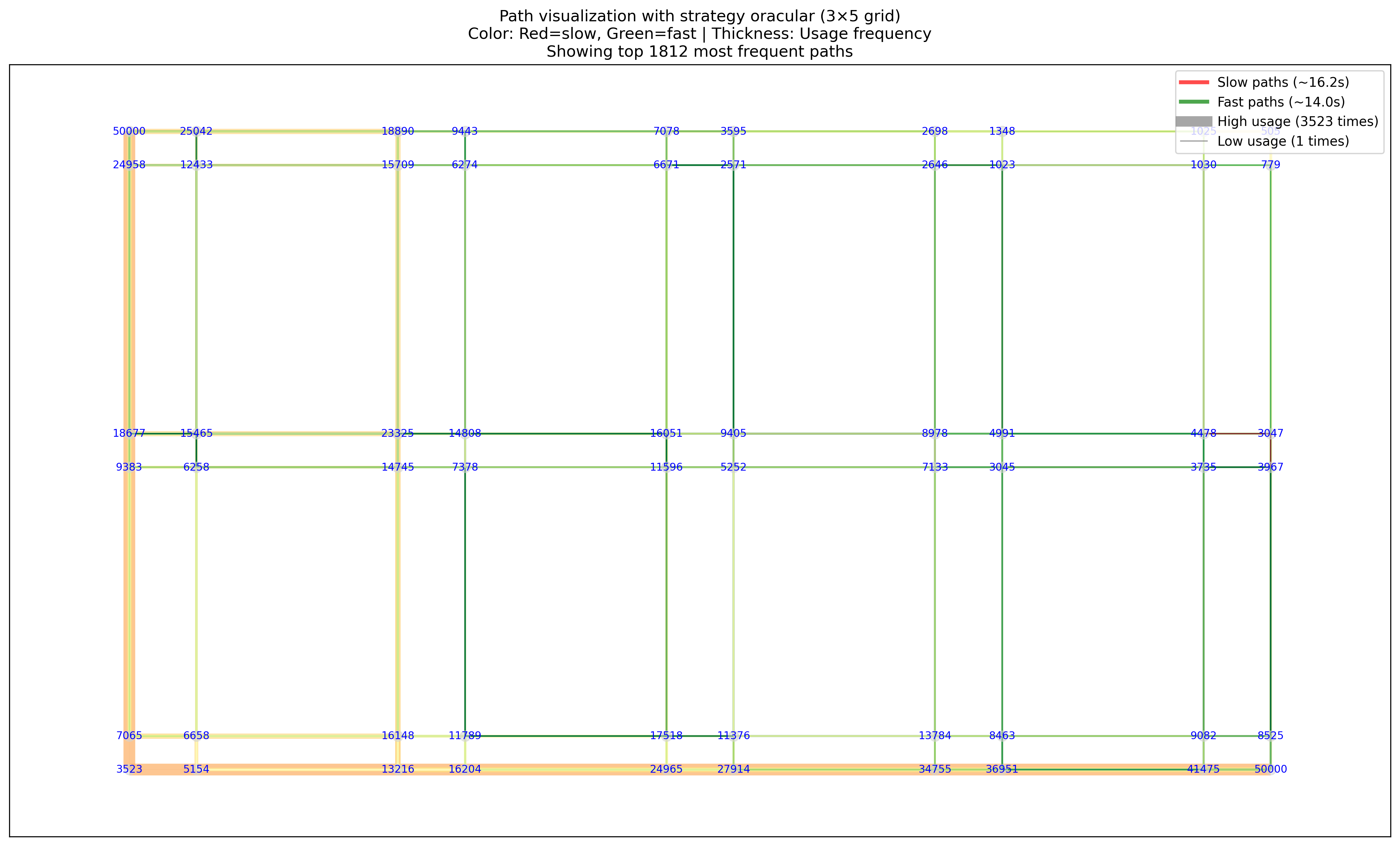
Oracular random. Note the symmetry just like the non-oracular random: we just pick, in the case where both directions are red, the faster, without prioritizing any direction.

[3] Source

joebhakim/street_crossing_sim.git

[4] FAQs

Is every light always visible to the walker?

• only the lights at the node the walker is currently at

There is no concern or penalty about the light turning red while in the middle of the street right? Like it's assumed a crossing is instant if the light is green at the start

• none whatsoever, just like real life, but no, there's a finite constant speed even in the crossing

[1] Strategy implementations

Dangerously vibecoded strategy implementations:

if strategy == Strategies.random:
    chosen = random.choice(move_data)
elif strategy == Strategies.oracular:
    # Perfect information strategy - choose minimum wait time
    chosen = min(move_data, key=lambda x: x['wait_time'])
elif strategy == Strategies.signal_observer:
    # Realistic strategy: observe current signal states
    green_moves = [m for m in move_data if m['is_green']]

    if len(green_moves) == 1:
        # Only one green signal - take it immediately
        chosen = green_moves[0]
    elif len(green_moves) > 1:
        # Multiple green signals - use balancing heuristic
        if end_node:
            e_remaining, s_remaining = calculate_remaining_moves(current_node, end_node)
            if e_remaining > s_remaining:
                # More east moves needed, prefer east
                east_green = [m for m in green_moves if m['direction'] == 'E']
                chosen = east_green[0] if east_green else random.choice(green_moves)
            elif s_remaining > e_remaining:
                # More south moves needed, prefer south
                south_green = [m for m in green_moves if m['direction'] == 'S']
                chosen = south_green[0] if south_green else random.choice(green_moves)
            else:
                # Equal remaining, choose randomly among green signals
                chosen = random.choice(green_moves)
        else:
            # No end node info, choose randomly among green signals
            chosen = random.choice(green_moves)
    else:
        # No green signals - wait for first one to turn green
        chosen = min(move_data, key=lambda x: x['wait_time'])
elif strategy == Strategies.edge:
    # Prefer eastward moves
    east_moves = [m for m in move_data if m['direction'] == 'E']
    chosen = random.choice(east_moves) if east_moves else random.choice(move_data)